Quiz 10.1:
Question:
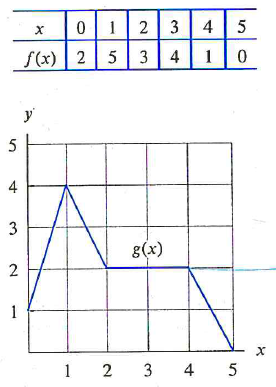
Use the table and figure below to,
5th Ed: #51
a) Calculate \( f(g(4)) \)
b) Solve \( g(g(x))=1 \)
b) Solve \( g(g(x))=1 \)
5th Ed: #51
Solution:
a) \( f(g(4) = f(2) = 3 \)
b)
b)
First find when \( g(x)= 1 \). That would be when \( x = 0 \) or \( x = 4.5 \)
Now we need to know when does \( g(x)= 0 , 4.5 \)
\( g(x) \neq 4.5 \) , but \( g(5) = 0 \) , so we have
\( g(g(5)= g(0) = 1 \)
Now we need to know when does \( g(x)= 0 , 4.5 \)
\( g(x) \neq 4.5 \) , but \( g(5) = 0 \) , so we have
\( g(g(5)= g(0) = 1 \)
