Quiz 9.6:
Question:
Find all three cube roots of \( i + 1 \) in both polar and cartesian form.
5th Ed: #35
5th Ed: #35
Solution:
First we write our complex number in polar form.
\( r = \sqrt{1^2+1^2} = \sqrt{2} \)
\( \theta = \tan ^{-1} \frac{1}{1} = \frac{\pi}{4} \)
Therefore \( 1+i = \frac{\sqrt{2}}{2} e^{\frac{\pi}{4}i} \)
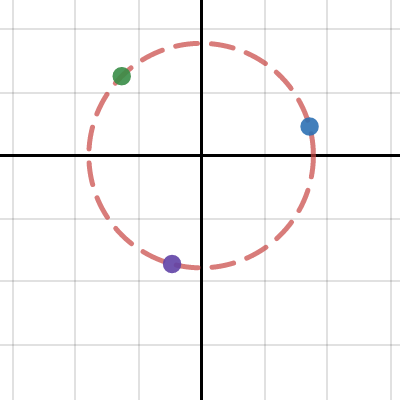
So our cube roots in polar form and Cartesian form respectively,
\( \left ( \sqrt{2} e^{\frac{\pi}{4}i} \right ) ^{\frac{1}{3}} = \sqrt[6]{2}e^{\frac{\pi}{12}i} = \sqrt[6]{2} \cos \left ( \frac{\pi}{12} \right ) + \sqrt[6]{2}i \sin \left ( \frac{\pi}{12} \right ) \)
\( \left ( \sqrt{2} e^{\frac{9\pi}{4}i} \right ) ^{\frac{1}{3}} = \sqrt[6]{2}e^{\frac{3\pi}{4}i} = \sqrt[6]{2} \cos \left ( \frac{3\pi}{4} \right ) + \sqrt[6]{2}i \sin \left ( \frac{3\pi}{4} \right ) \)
\( \left ( \sqrt{2} e^{\frac{17\pi}{4}i} \right ) ^{\frac{1}{3}} = \sqrt[6]{2} \cos \left ( \frac{17\pi}{12} \right ) + \sqrt[6]{2} i\sin \left ( \frac{17\pi}{12} \right ) \)
\( r = \sqrt{1^2+1^2} = \sqrt{2} \)
\( \theta = \tan ^{-1} \frac{1}{1} = \frac{\pi}{4} \)
Therefore \( 1+i = \frac{\sqrt{2}}{2} e^{\frac{\pi}{4}i} \)
So our cube roots in polar form and Cartesian form respectively,
\( \left ( \sqrt{2} e^{\frac{\pi}{4}i} \right ) ^{\frac{1}{3}} = \sqrt[6]{2}e^{\frac{\pi}{12}i} = \sqrt[6]{2} \cos \left ( \frac{\pi}{12} \right ) + \sqrt[6]{2}i \sin \left ( \frac{\pi}{12} \right ) \)
\( \left ( \sqrt{2} e^{\frac{9\pi}{4}i} \right ) ^{\frac{1}{3}} = \sqrt[6]{2}e^{\frac{3\pi}{4}i} = \sqrt[6]{2} \cos \left ( \frac{3\pi}{4} \right ) + \sqrt[6]{2}i \sin \left ( \frac{3\pi}{4} \right ) \)
\( \left ( \sqrt{2} e^{\frac{17\pi}{4}i} \right ) ^{\frac{1}{3}} = \sqrt[6]{2} \cos \left ( \frac{17\pi}{12} \right ) + \sqrt[6]{2} i\sin \left ( \frac{17\pi}{12} \right ) \)

