Quiz 4.2:
Question:
The following graph shows the voltage, \(V(t) \), across a circuit element at time \(t\) seconds. For \(t<0 \), the voltage is a constant 60 volts; for \( t \geq 0 \) the voltage decays exponentially.
Find a piecewise formula for \(V(t) \).
Find a piecewise formula for \(V(t) \).
Solution:
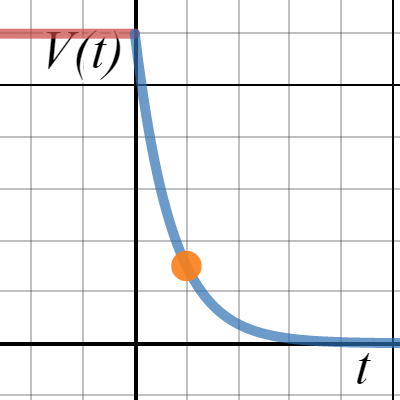
Since the funcion starts out constant, we know that \(V(t)=60 , t<0 \).
Now we need to solve for \(a\) and \(b\) in the exponential portion.
\( V(t)=\left\{\begin{matrix}60 & ,t<0\\ a(b)^t &,t \geq 0 \end{matrix}\right. \)
We know the initial voltage is 60, so we know that \(a=60\)
We know that at time \(t=10\), \(V=15\),
Now we need to solve for \(a\) and \(b\) in the exponential portion.
\( V(t)=\left\{\begin{matrix}60 & ,t<0\\ a(b)^t &,t \geq 0 \end{matrix}\right. \)
We know the initial voltage is 60, so we know that \(a=60\)
We know that at time \(t=10\), \(V=15\),
\( 15=60 (b)^{10} \)
\( \frac{1}{4}=b^{10} \)
\( b= \sqrt[10]{\frac{1}{4}} \)
\( V(t)=\left\{\begin{matrix}60 & ,t<0\\ 60 \left ( \sqrt[10]{\frac{1}{4}} \right )^t &,t \geq 0 \end{matrix}\right. \)\( \frac{1}{4}=b^{10} \)
\( b= \sqrt[10]{\frac{1}{4}} \)
