Quiz 3.1/3.2:
Question:
Given the quadratic function \( q(x) = -2x^2-2x+12 \)
a) Write the function in factored form.
b) Write the function in vertex form.
c) Give the vertex.
d) Find the y-intercept.
e) Discuss the concavity.
f) Sketch the graph.
b) Write the function in vertex form.
c) Give the vertex.
d) Find the y-intercept.
e) Discuss the concavity.
f) Sketch the graph.
Solution:
a) \( q(x)=-2 \left ( x^2+x-6 \right ) \)
\( q(x) = -2 (x+3)(x-2) \)
b) \( q(x) = -2 \left ( x^2 +x + \frac{1}{4} -6 - \frac{1}{4} \right ) \)
\( q(x) = -2 \left ( \left ( x+\frac{1}{2} \right ) ^2 - \frac{25}{4} \right ) \)
\( q(x) = -2 \left ( x + \frac{1}{2} \right ) ^2 + \frac{25}{2} \)
c) Vertex at \( \left ( -\frac{1}{2} , \frac{25}{2} \right ) \)
d) \( q(0) = 12 \)
e) Concave down over its entire domain, since the lead coefficient is negative.
f)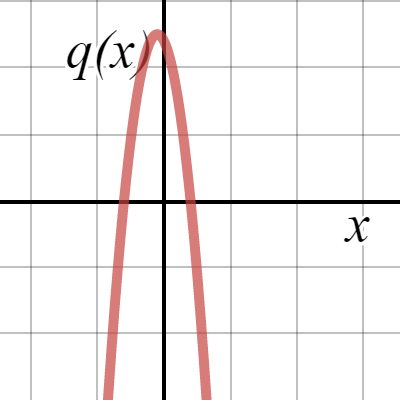
\( q(x) = -2 (x+3)(x-2) \)
b) \( q(x) = -2 \left ( x^2 +x + \frac{1}{4} -6 - \frac{1}{4} \right ) \)
\( q(x) = -2 \left ( \left ( x+\frac{1}{2} \right ) ^2 - \frac{25}{4} \right ) \)
\( q(x) = -2 \left ( x + \frac{1}{2} \right ) ^2 + \frac{25}{2} \)
c) Vertex at \( \left ( -\frac{1}{2} , \frac{25}{2} \right ) \)
d) \( q(0) = 12 \)
e) Concave down over its entire domain, since the lead coefficient is negative.
f)

